首先,什么是级数求和呢?我讲内容,总是喜欢让大家先有了直观感受,再随之深入研究。
下面的自然数求和,它等于多少呢?
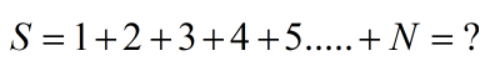
它等于多少呢?
也许你曾看见过这样离谱的答案:
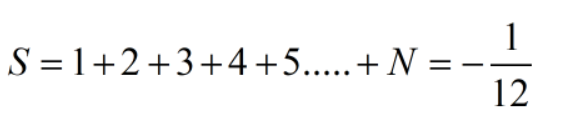
有些民科为了这个问题提出了自己的见解,但说不出个所以然,不谈公式的适用范围而乱用公式,就是耍流氓。
这个只有黎曼空间中才能成立,我们叫做解析延拓,但是今天我们不讲这个,只是让大家先看一下它的奇怪性质。

黎曼
我们再来看一个好玩的:
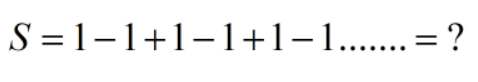
它该等于多少呢?
再比如这个相当经典的级数,我们把它称为调和级数:
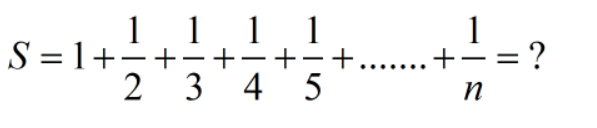

事实上,显而易见,上面的问题根本就没有答案,它们要么是趋于无穷的,要么就是在振荡,我们把这种算不出结果,振荡或趋于无穷大的级数称为发散。
以后你再听到发散这个词,脑袋中就有“疯狂跳变”,“无穷大”,“没办法算”这样的感觉了。
接着,我们来讲讲求和符号:
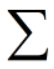
有时候,你会看到这样的公式:
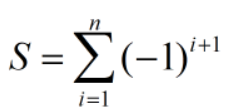
它是1-1+1....的简写和缩写
你一下子慌了神:“我的天,好复杂啊!”
其实并不复杂,它代表了一长串小公式合到一块儿写成的大公式:
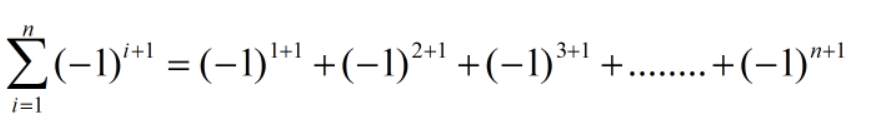
把I=1234....依次往里面带
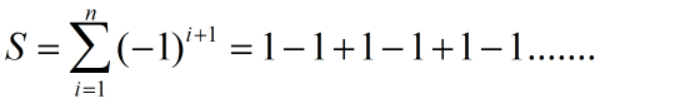
只是写法不同而已
我们再来:
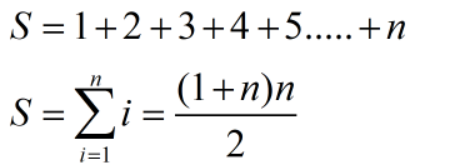
两者等价,是一个意思
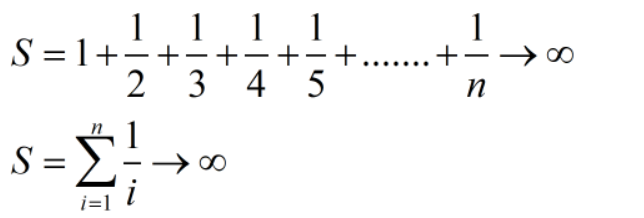
两者等价,是一个意思
讲完了发散,让我们来聊聊可以求和的级数:
下面是一个相当著名的欧拉级数:当-1<X<1时(注意定义域)
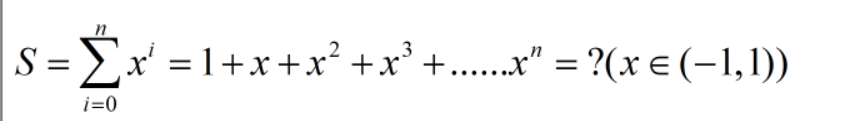
我们用等比数列求和法则,可以得到:
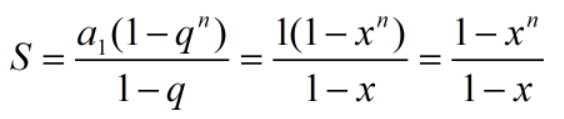
一个小数的无穷大次方将趋于0:
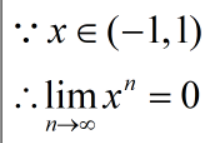
所以,我们可以化简为:
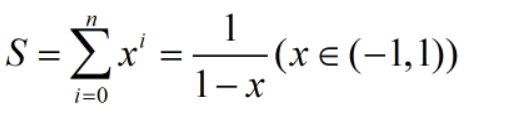
这个公式有什么用呢?比如:
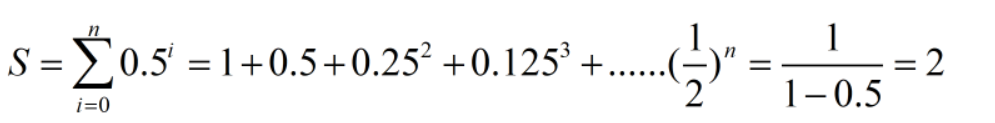
这不正是芝诺飞矢不动悖论的解吗?
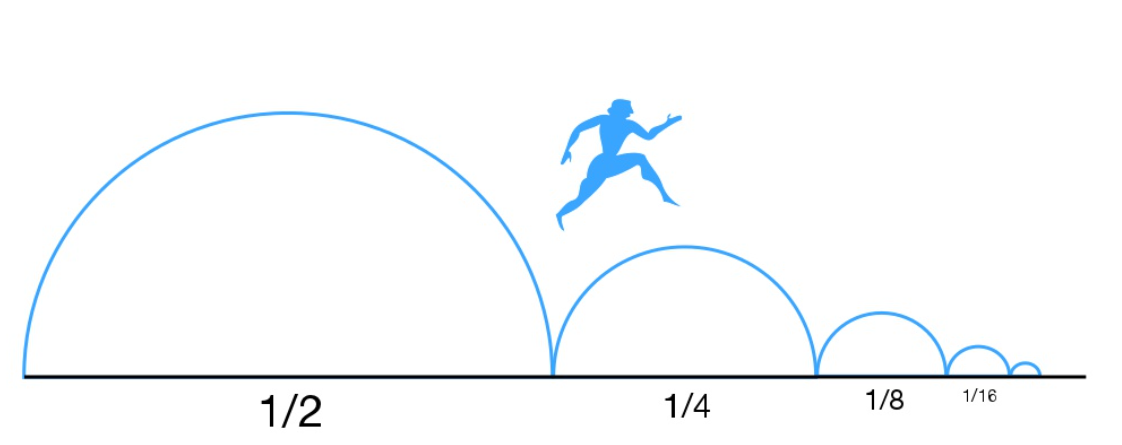

于是,我们把这种可以求和的级数称作“收敛”级数。收敛的大致意思就是说我们能求出级数加起来的那个最终结果值(无限逼近)。
级数相生相克,又藕断丝连。可谓取之不尽,用之不竭。